Online capacity estimation of lithium-ion batteries with deep long short-term memory networks

In this post, I review the recently published paper “Online capacity estimation of lithium-ion batteries with deep long short-term memory networks” by Li, Sengupta, Dechent, Howey, Annaswamy, and Sauer.

Note: this review was completely reworked based on the input from Weihan Li, the author of the paper. Thanks to him for helping to fix my understanding.

---

Summary: an LSTM-RNN model was trained to estimate the remaining (degraded) cell capacity using as inputs just time-stamped voltage readings during charging cycles.

The promise of the paper is to make the estimation simpler. The authors achieve that: they use absolutely minimum inputs to the model and don’t require any computation before feeding this input into the LSTM-RNN model.

After cycling several cells while estimating their capacity, here are the best and worst (left-right) results:

© Elsevier. Estimated capacity of the model: left—best cell, right—worst cell.

© Elsevier. Absolute Percentage Error (APE) of the model, relative to “Reference”

Note: the abrupt jumps in estimated capacity on the charts above are not arbitrary defects of the estimation model. The jumps are caused by actual cell capacity recovery during rest (during cell characterisation events, in this case). The smoothed "Reference" lines on the charts are not the actual cell capacities, but an interpolation of the cell capacities as measured during the characterisation events. Therefore, the actual error of the LSTM model is smaller than it is shown on the lower charts.

The LSTM model was trained with the loss function of the mean average error (MAE) relative to the "Reference". Because of this, we see that the model overestimates the capacity at the characterisation points (the only points where the "Reference" is the actual capacity) in order to minimise MAE over the whole history. The model would produce even better results if it was trained against more truthful capacity reference which would have discontinuities at the characterisation points, like this:

Picture from this paper

The model that uses only the voltage signal can't identify and fix sensor bias

Notice that the worst-performing cell estimation consistently underestimates the remaining capacity:

© Elsevier. Estimated capacity of the model: left—best cell, right—worst cell.

This might be due to biased sensor data, or because the worst cell had markedly higher internal resistance than the other cells in the training set. In theory, the LSTM model could have learned about cells with different internal resistances to estimate their capacity better (although it would be much easier to do this if we fed the internal resistance into the LSTM model as a separate input). However, the model has absolutely no means to detect voltage measurement bias because this is the only sensor input it receives.

The authors used only voltage as an input for the model because they cycled cell at a constant current.

In real-world applications (or further research), would be interesting to have a neural network trained with voltage, current, and temperature measurements, learning how the sensor biases look like and relate to other measurements, and make unbiased state-of-health estimations from biased inputs completely by itself. Perhaps, we can integrate this idea with a stochastic cell parameter estimator based on an electrical cell model.

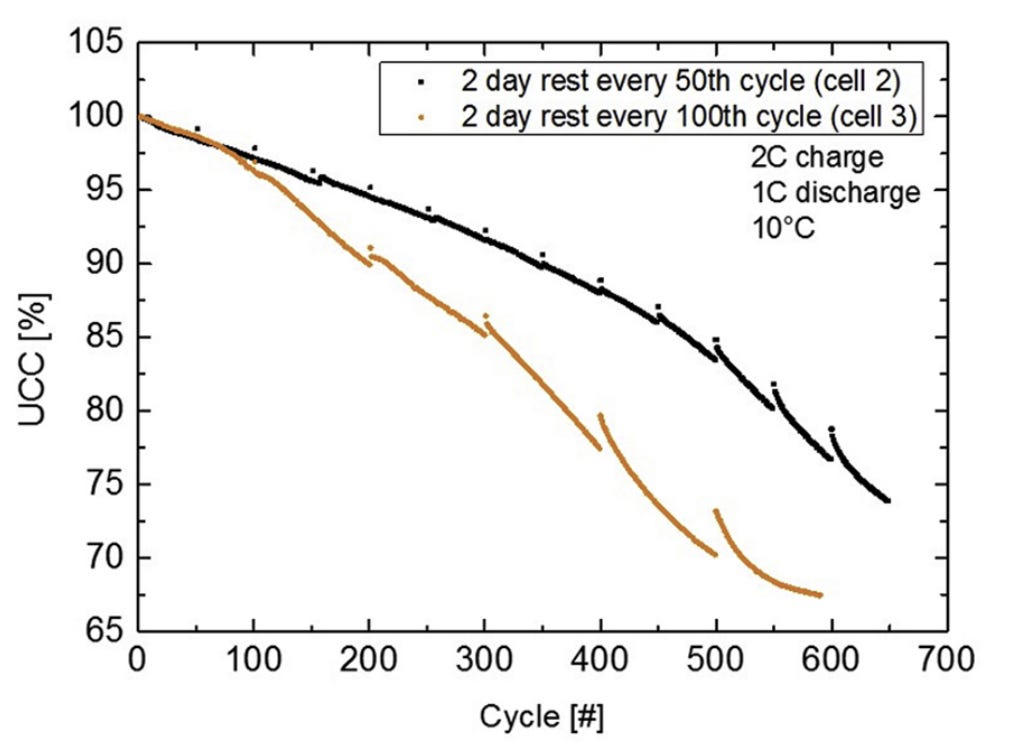
There is no correlation between the cell’s initial capacity and the future lifetime

This is an interesting observation made by the authors while they cycled the cells to get the data for their LSTM model:

© Elsevier